forum.alglib.net

Good day all!

I am using alglib-3.16.0.csharp.

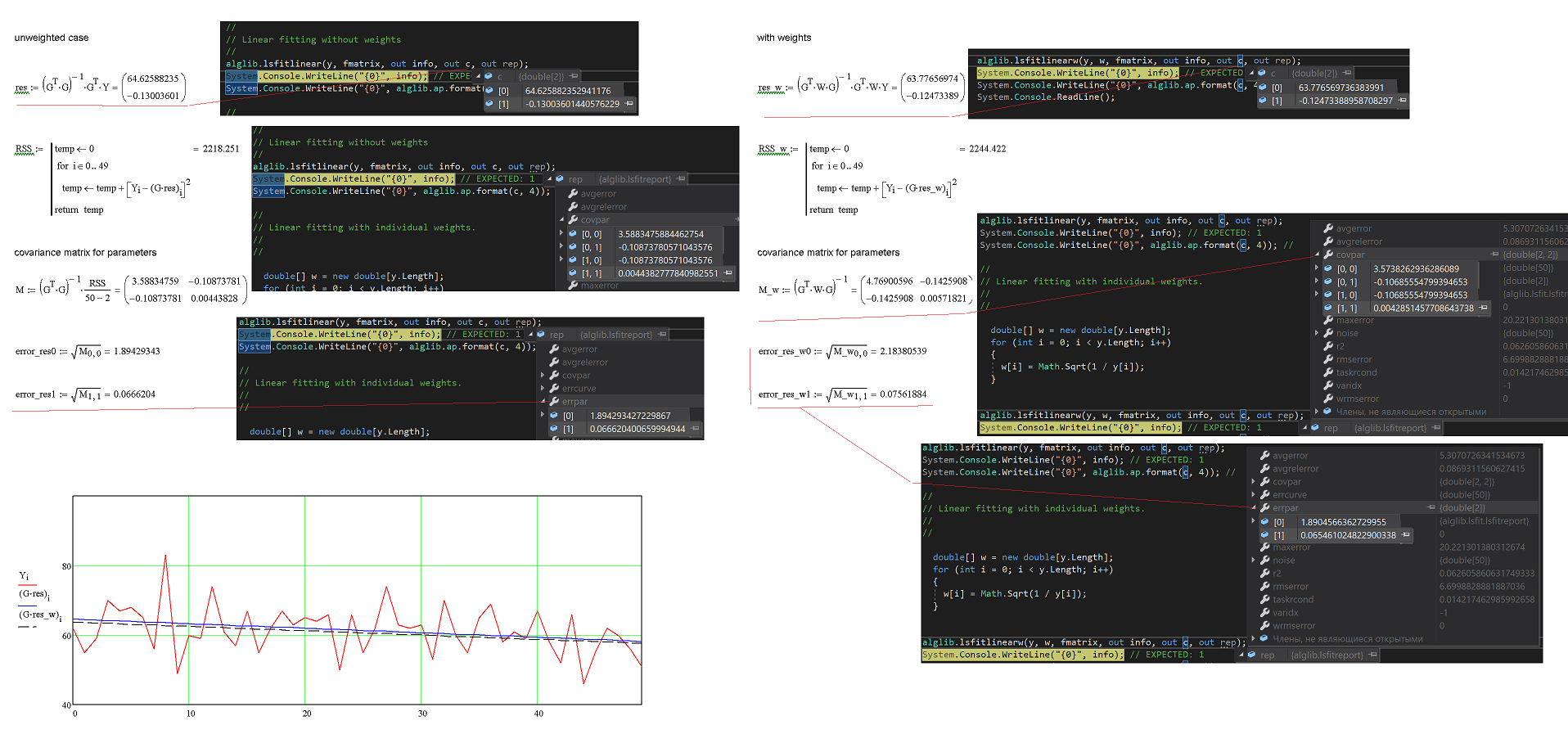
There are relatively simple equations to solve unweighted linearly
least square problem Y = X * b:
b = (XT * X)-1 * XT * Y
covariance matrix for parameters b is M = RSS / ( n - 2) * (XT * X)-1. RSS - Residual Sum of Squares. The numerator, n−p, is the statistical degrees of freedom. In case for line n - 2.

and for the weighted linearly least square
b = (XT * W * X)-1 * XT * W * Y, where W - diagonal matrix
covariance matrix for parameters b is M = (XT * W * X)-1

In both cases, the variance of the parameter bi is given by Sqrt(Mii).

https://en.wikipedia.org/wiki/Weighted_least_squares

For unweighted case Alglib's results are equal whith results from equations before: parameters b and covariance matrix M. Сomplete match.
But for weighted case only results for parameters b are equal whith results from equations before. The covariance matrix, in turn, differs from the equation above.


Can someone tell me what's the matter?





// This is my task
//------------------------------------------------------------------------------------------------------------------------------------------
// data points Y
double[] y = new double[] { 62, 55, 59, 70, 67, 68, 65, 56, 83, 49, 60, 59, 74, 61, 57, 67, 55, 62, 67, 63, 65, 64, 66, 50, 66, 55, 62, 74, 63, 62, 63, 53, 70, 60, 55, 65, 69, 58, 61, 59, 67, 58, 52, 66, 46, 55, 62, 60, 56, 51 };

// data points X from 0 to 49.

double[,] x = new double[y.Length, 1];

for (int i = 0; i < y.Length; i++)
{
x[i, 0] = (double)(i);
}

// data points will be fitted by line function: Y = c[0] + c[1] * X

// Fmatrix forming

double[,] fmatrix = new double[y.Length, 2];

// all fmatrix[i, 0] = 1. This is for c[0]

for (int i = 0; i < y.Length; i++)
{
fmatrix[i, 0] = 1;
}

// fmatrix[i, 1] = X[i]. This is for c[1]

for (int i = 0; i < y.Length; i++)
{
fmatrix[i, 1] = x[i, 0];
}

int info;
double[] c;
alglib.lsfitreport rep;

//
// Linear fitting without weights
//
alglib.lsfitlinear(y, fmatrix, out info, out c, out rep);
System.Console.WriteLine("{0}", info); // EXPECTED: 1
System.Console.WriteLine("{0}", alglib.ap.format(c, 4));

//
// Linear fitting with individual weights.
//
//

// in my case variance(Y[i]) = Y[i], so I combine vector w[i] as
double[] w = new double[y.Length];
for (int i = 0; i < y.Length; i++)
{
w[i] = Math.Sqrt(1 / y[i]);
}

alglib.lsfitlinearw(y, w, fmatrix, out info, out c, out rep);
System.Console.WriteLine("{0}", info); // EXPECTED: 1
System.Console.WriteLine("{0}", alglib.ap.format(c, 4));
System.Console.ReadLine();

//-----------------------------------------------------------------------------------------------------------

Best regards

I have done a little research and can answer my own question.
Y = X * b
parameters with minimal RSS: b = (XT * X)-1 * XT * Y
covariance matrix for parameters b: exact form M = (XT * X)-1 * X * K * X * (XT * X)-1, where K is covariance matrix for Y.
But if you do not know K and suppose that Kii = sigma^2 (homoscedastic case, K = sigma^2 * I, M = (XT * X)-1 * XT * K * X * (XT * X)-1 = sigma^2 * (XT * X)-1 * XT * I * X * (XT * X)-1 = sigma^2 * (XT * X)-1) than you could calculate a tally for sigma^2 from RSS: sigma*^2 = RSS / ( n - 2).
So a tally M = RSS / ( n - 2) * (XT * X)-1. RSS - Residual Sum of Squares. The numerator, n−p, is the statistical degrees of freedom. In case for line n - 2.

For weighted least square the same is true.
You know about heteroscedasticity in your data. You choose W matrix, which in ideal case is equal to K-1.
b = (XT * W * X)-1 * XT * W * Y and covariance matrix for parameters b is M = (XT * W * X)-1.
If you do no know the ecxact form of K, but have some good tally for K (or you know relation between errors for Yi) you can transform the original equation (Y = X * b) into a new homoscedastic one by multiplying by the W matrix.
And the new equation Y_ = X_ * b will have the same solution (b) and like before (for OLS) you can tally M matrix: M = RSS / ( n - 2) * (X_T * X_)-1.

Thus alglib evaluates the covariance matrix from the data itself. This is the typical way for a computing software.

p.s. alglib do the same for none-linear least square problem (evaluates the covariance matrix from the data itself), I cheked it.
If you want tot use your tally for K-matrix not only to solve equation but rather for covariance matrix of parameters evaluation you need calculate M by yourself.